Numerography

This website blog chronicles my exploration into using symbology to represent alternative numerical base systems. My ultimate goal is to uncover and simplify known, and unknown, mathematical processes and connections between these systems. This is a hobby and should be taken as such. Thanks for visiting.

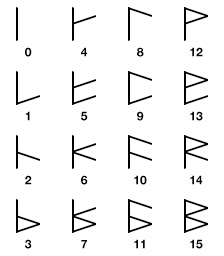
027 Binquadric Finger Counting & Adding

2008-07-20 Filed in: Binquadric
Let’s examine some alternative systems for adding Binquadric numbers.


Binquadric_8 bin_palm

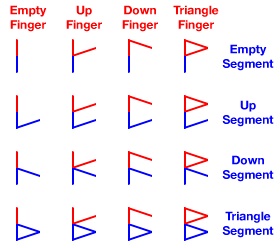
Binquadric_9z
The example above shows 16 areas that the left thumb can point to on it’s own hand. To add using this method, we will need to memorize the glyphs associated with those areas.


One way to possibly make it easier to memorize the associations is to break up the glyph into two pieces. The top portion of the glyph tells you the finger, while the bottom portion tells you the knuckle, (or segment).

ex. If the top looks like a triangle, then it’s on the pinky finger...

A similar method could be worked out to identify the bottom portion. Though it’s helpful for beginners, having a system to help you figure out what glyph goes where, it might just be easier to create some flash cards and memorize the positions. For experimenting purposes, I have sometimes drawn the glyphs on a glove. For the purposes of learning these concepts, simply use the illustrations provided.


Binquadric_add_3i
Let’s look at this example. Here we have two binquadric numbers that we want to add. The first column is easy. There are no overlapping binary sub digits, so we can just combine the glyphs together.

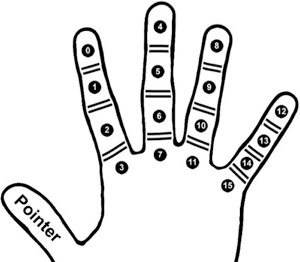
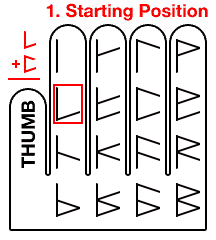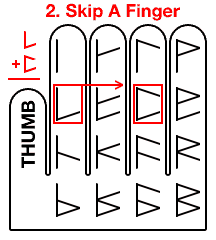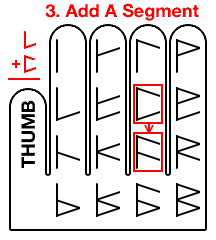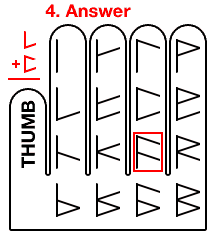
The next column is trickier though. The first step is to locate the position on the hand that’s associated with the first glyph.



bin01v1
Hold your left palm open and facing upwards. Use the chart above, or the system discussed previously, to find the starting position. That places the starting position on the forefinger, but shifted downward one segment.

bin09v1
Let’s look at the second number. Examine the binary sub digits of the second number. It translates to 1001. This tells us how to move the thumb from the starting position.


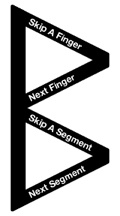
Binquadric_7
There are four binary sub digits in a Binquadric number, and each one has a simple rule. By using these rules, we can quickly add the numbers together using the thumb as a pointer.

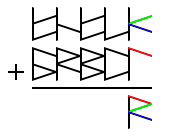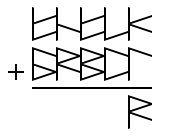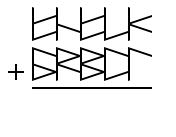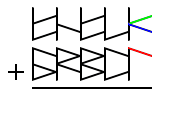
Upper Top = skip or jump over one finger.

Upper middle = slide to the next finger.

Lower middle = skip or jump over one segment.

Lower Bottom = slide to the next segment.



Binquadric_9
Place your left thumb on the starting position. Then examine the second glyph. It contains an upper binary sub digit. To add the upper sub digit, we move the thumb two finger positions, or, as I like to think of it, we skip, or jump over a finger position.

There are no middle sub digits, but there is a bottom sub digit. This indicates a movement of one segment. So we slide the thumb downwards to the next segment.

The ending position is our answer. We write this glyph down and continue to the next column.

Of course, it’s probably worth mentioning that if you switched the glyphs around, starting with the second glyph and then added the first glyph, the operation would have been much simpler. Just as in decimal addition, the mind will eventually work out shortcuts with practice.



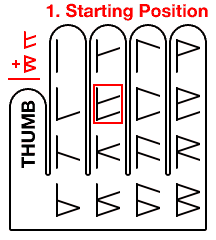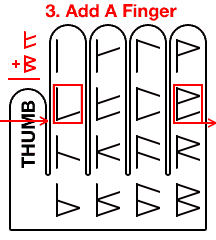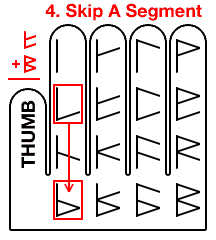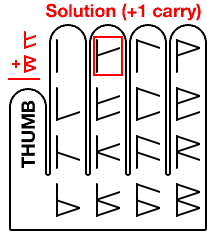
Binquadric_9b
Onto the next column. Find the starting position and touch your thumb to it.
We skip a finger over to the pinky finger, (representing the upper top sub digit).

Then we proceed to add one finger, (representing the upper middle sub digit), but we find that we’ve run out of fingers. So, we jump back to the forefinger, and commit to memory that we will need to ‘carry one’.

Then we skip a segment, (represented by the lower sub digit), landing us on the callused pad at the base of the forefinger.

Now we just need to add just one more segment, (represented by the bottom sub digit). We jump back to the top of the finger, but this time, we shift over to the next finger. This extra shift represents our ‘carry one’, so we do not have to commit this carry to memory.

There’s our answer, ‘carry one’ plus the fifth segment. If we were to translate what we’ve done into mainstream hexadecimal, we’d find that we just calculated: 5 + F = 14

Just as in the last column that we added, there is also a shortcut here. In decimal, some people use a shortcut when adding nine. To figure out seven plus nine, they take seven minus one and place a one in front. The same thing can be done when adding F. There are numerous shortcuts that can be used, but after enough use, you’ll find that for faster calculations, it’s worth it to memorize the entire addition table.

Tags: ,