025 Binquadric Sub-Digit Addition
2008-07-15 Filed in: Binquadric
There’s a few different methods for adding in Binquadric.
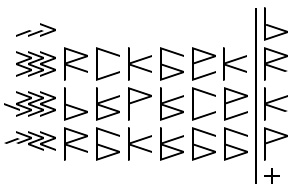
One easy method for complete beginners is to add the binary sub digits, one at a time. This is not the fastest method, but it is the the most basic method.
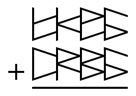
Let’s look at this example. Here we have two binquadric numbers that we want to add together, 56DB + 9EFB. We could just convert it to binary, and add it: 101011011011011 + 1001111011111011. But there is a way to add the sub digits without changing the structure.
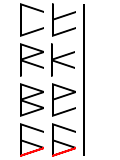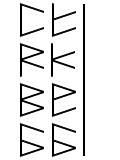
Let’s start by writing the digits vertically. The numbers now read from top to bottom, that is to say that first digit starts at the bottom, and higher digits are written above. This lines up all the sub binary digits next to each other, making it much easier to add. Starting at the bottom, we see that one will have to be added to one. In binary, this equals 10. So, whenever you need to add two ones, just think zero and carry one.
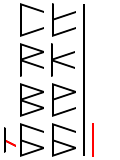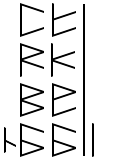
So we create a staff on the right, but we don’t draw in a digit. This represents the zero. Then we have to deal with the ‘carry over’. Just as in decimal addition, we write it into the sequence in the next digit, or in this case, sub digit.
We draw a smaller staff to the left, and place a backslash into the next sub digit line. This ‘carry over’ will be added together with the other backslashes in the secondary sub digit places.
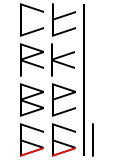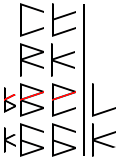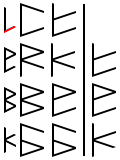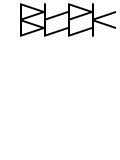
When we look at the ones in the secondary sub digit places, we find that there are three. The sum of three ones in binary is 11. So our next step will be to draw a backslash into our solution column on the right, and then to carry the other one up to the next sub digit.
The pattern becomes obvious at this point. You just have to remember four basic summations. 0+0=0; 0+1=1; 1+1=10; 1+1+1=11
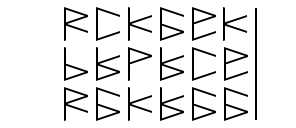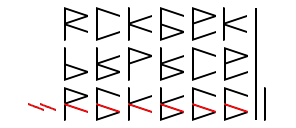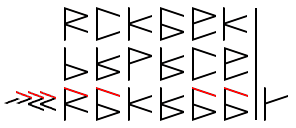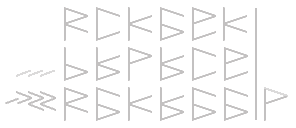
Here we see an example of how someone could add multiple numbers using this method. For every two lines that appear when adding across, a new line is carried up to the next row. This process is easy to perform, but there are faster ways to add if you’re willing to invest some time into more complex methods.

