011 Three Dimensional Direction & Location
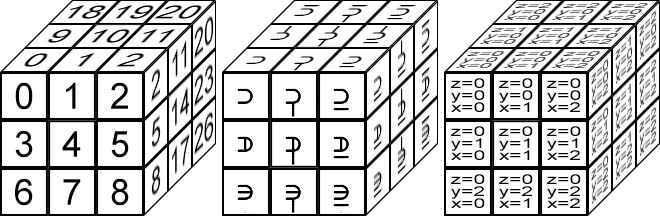
The sample above shows all 27 cubes, named 0 to 26.
A Trincubic numeral use three ternary sub-digits. If we assign those sub-digits to each of those cubes, we can create a system of three dimensional location.
I would recommend that a fractional system be employed. Similar to the use of a Decimal Point in Decimal, we will use a Trincubic Point in Trincubic. The idea is to create a system that can progressively narrow down the coordinates of a specific area in a finite area of space.
For example, if I were to say that an object was located somewhere in .2 Trincubic, I would mean that an object was located somewhere in the rightmost third of an area, the frontmost third of an area, and the upwards most third of an area. In other words, if we were to map an imaginary Rubik’s cube to an area, the object would be in the sub-cube labeled 2 in the above example.
If we wanted to figure out a more precise location, we could map a secondary Rubik’s cube to the .2 cube to specify a more accurate position. This method can continue for as many places as necessary.
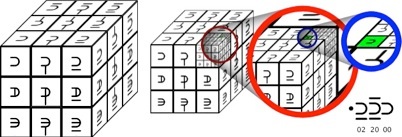
This example, zooms in on a location that can be defined by three trincubic digits; 2, 20, and 0. Trincubics allows us to define positions in a three dimensional space using only one number.
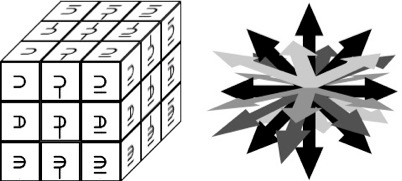
Another useful feature of Trincubic numbers is directional reference. Every numeral, (except 13), represents a direction. Direction is defined by the start point of the center sub-cube, (13), to one of the outer sub-cubes.

